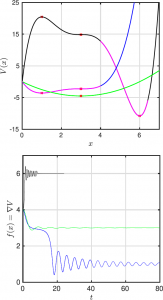
In the present work we explore the application of a few root-finding methods to a series of prototypical examples. The methods we consider include: (a) the so-called continuous time Nesterov (CTN) flow method; (b) a variant thereof referred to as the squared-operator method (SOM); and (c) the joint action of each of the above two methods with the so called deflation method. More “traditional” methods such as Newton’s method (and its variant with deflation) are also brought to bear. Our toy examples start with a naive one degree-of-freedom (DOF) system to provide the lay of the land. Subsequently, we turn to a 2-DOF system that is motivated by the reduction of an infinite-dimensional, phase field crystal (PFC) model of soft matter crystallisation. Once the landscape of the 2-DOF system has been elucidated, we turn to the full PDE model and illustrate how the insights of the low-dimensional examples lead to novel solutions at the PDE level that are of relevance and interest to the full framework of soft matter crystallisation.

arXiv Journal