Spatial localisation beyond steady states in the neighbourhood of the Takens-Bogdanov bifurcation
Alrihieli, H., Rucklidge, A.M., & Subramanian, P.
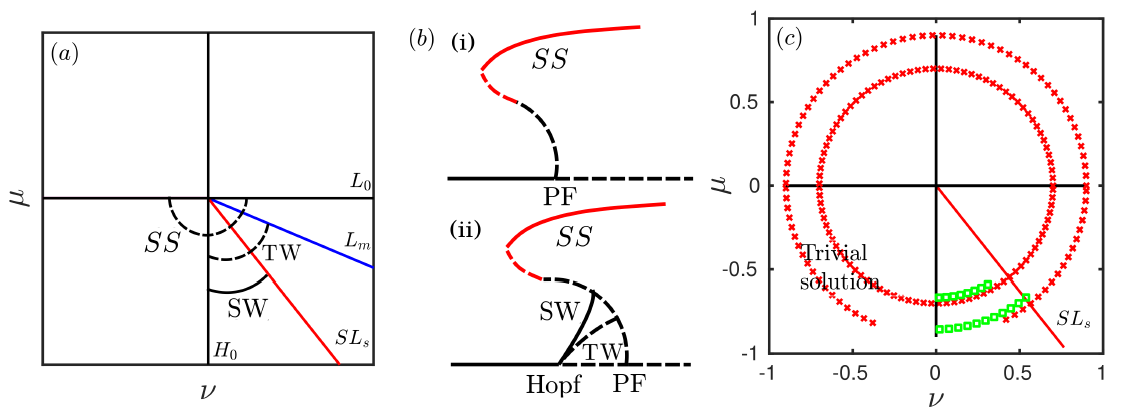
The coincidence of a pitchfork and Hopf bifurcation at a Takens–Bogdanov bifurcation occurs in many physical systems such as double-diffusive convection, binary convection and magnetoconvection. Analysis of the associated normal form, in one dimension with periodic boundary condition, shows the existence of steady patterns, standing waves, modulated waves and travelling waves, and describes the transitions and bifurcations between these states. Values of coefficients of the terms in the normal form classify all possible different bifurcation scenarios in the neighbourhood of the Takens–Bogdanov bifurcation (Dangelmayr & Knobloch, 1987). In this work we develop a new and simple pattern-forming PDE model, based on the Swift–Hohenberg equation, adapted to have the Takens–Bogdanov normal form at onset. This model allows us to explore the dynamics in a wide range of bifurcation scenarios, including in domains much wider than the lengthscale of the pattern. We identify two bifurcation scenarios in which coexistence between different types of solutions is indicated from the analysis of the normal form equation. In these scenarios, we look for spatially localised solutions by examining pattern formation in wide domains. We are able to recover two types of localised states, that of a localised steady state in the background of the trivial state and that of a spatially localised travelling wave in the background of the trivial state which have previously been observed in other systems. Additionally, we identify two new types of spatially localised states: that of a localised steady state in a modulated wave background and that of a localised travelling wave in a steady state background. The PDE model is easy to solve numerically in large domains and so will allow further investigation of pattern formation with a Takens–Bogdanov bifurcation in one or more dimensions and the exploration of a range of background and foreground pattern combinations beyond steady states.
